Первый закон Кеплера (Закон эллипсов)

Первый закон Кеплера.
Каждая планета Солнечной системы обращается по эллипсy, в одном из фокусов которого находится Солнце.
Форма эллипса и степень его сходства с окружностью характеризуется отношением 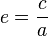 , где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.
, где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.
Второй закон Кеплера (Закон площадей)

Второй закон Кеплера.
Каждая планета движется в плоскости, проходящей через центр
Солнца, причём за равные времена радиус-вектор, соединяющий Солнце и
планету, заметает сектора равной площади.
Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий
— наиболее удалённая точка орбиты. Таким образом, из второго закона
Кепплера следует, что планета движется вокруг Солнца неравномерно, имея
в перигелии бо́льшую линейную скорость, чем в афелии.
Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике
к востоку также происходит быстрее, чем в среднем за год. В начале июля
Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца
по эклиптике замедляется. Закон площадей указывает, что сила,
управляющая орбитальным движением планет, направлена к Солнцу.
Третий закон Кеплера (Гармонический закон)
Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.
 , где T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит.
, где T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит.
Ньютон установил, что гравитационное притяжение
планеты определенной массы зависит только от расстояния до неё, а не от
других свойств, таких, как состав или температура. Он показал также,
что третий закон Кеплера не совсем точен — в действительности в него
входит и масса планеты:  , где M – масса Солнца, а m1 и m2 – массы планет.
, где M – масса Солнца, а m1 и m2 – массы планет.
Поскольку движение и масса оказались связаны, эту комбинацию
гармонического закона Кеплера и закона тяготения Ньютона используют для
определения массы планет и спутников, если известны их орбиты и
орбитальные периоды.
Современный уточненный третий закон Кеплера, учитывая
эксцентриситеты орбит, дает самую большую точность расчетов по небесной
механике и астрофизике: 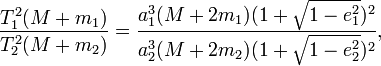 где e1,e2 - эксцентриситеты орбит.
где e1,e2 - эксцентриситеты орбит.




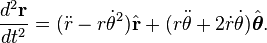


 и
и  во второе уравнение, получим
во второе уравнение, получим 




 , которая является удельным угловым моментом (
, которая является удельным угловым моментом (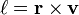 ).Пусть
).Пусть 

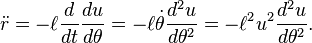
 становится равным
становится равным 
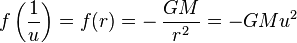

![u = \frac{GM}{\ell^2} \left[ 1 + e\cos(\theta-\theta_0) \right] .](http://upload.wikimedia.org/math/e/1/d/e1de7bd8772f6b459768424ccab8e86c.png)

 точечной частицы с массой
точечной частицы с массой  записывается в виде:
записывается в виде: 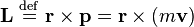 .
. - радиус-вектор частицы а
- радиус-вектор частицы а  - импульс частицы.
- импульс частицы. 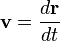 .
. .
.
 - константа.
- константа. 













 (что равно
(что равно  ). Время полного оборота, таким образом, равно
). Время полного оборота, таким образом, равно 





