Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.
Формулировка
Пусть постоянный ток  течёт по контуру γ, находящемуся в вакууме,
течёт по контуру γ, находящемуся в вакууме,  — точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом
— точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом
Направление  перпендикулярно
перпендикулярно  и
и 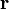 , то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление
, то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление  , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора
, если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора  определяется выражением
определяется выражением
Векторный потенциал даётся интегралом
Вывод из уравнений Максвелла
Закон Био — Савара — Лапласа может быть получен из уравнений Максвелла для стационарного поля. При этом производные по времени равны 0, так что уравнения для поля в вакууме примут вид
где  — плотность тока
в пространстве. При этом электрическое и магнитное поля оказываются
независимыми. Воспользуемся векторным потенциалом для магнитного поля:
— плотность тока
в пространстве. При этом электрическое и магнитное поля оказываются
независимыми. Воспользуемся векторным потенциалом для магнитного поля:
Калибровочная инвариантность уравнений позволяет наложить на векторный потенциал одно дополнительное условие:
Раскрывая двойной ротор по формуле векторного анализа, получим для векторного потенциала уравнение типа уравнения Пуассона:
Его частное решение даётся интегралом, аналогичным ньютонову потенциалу:
Тогда магнитное поле определяется интегралом
аналогичным по форме закону Био — Савара — Лапласа. Это соответствие можно сделать точным, если воспользоваться обобщёнными функциями и записать пространственную плотность тока, соответствующую витку с током в пустом пространстве. Переходя от интегрирования по всему пространству к повторному интегралу вдоль витка и по ортогональным ему плоскостям и учитывая, что
получим закон Био — Савара — Лапласа для поля витка с током.


![\mathbf B = {\mu_0 \over 4\pi} \int\limits_\gamma \frac{I[d\mathbf{l};\mathbf{r} - \mathbf{r}_0]}{|\mathbf r - \mathbf{r}_0 |^3}](http://upload.wikimedia.org/math/e/d/f/edf5ad6293d164dedb21f663ac7d26f9.png)

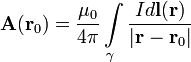

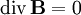
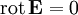

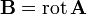

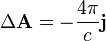
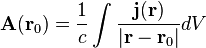
![\mathbf B = \operatorname{rot}\,\mathbf A =
\frac{1}{c} \int \left[ \nabla \frac{1}{|\mathbf r - \mathbf r_0|} ; \mathbf j(\mathbf r) \right] dV =
\frac{1}{c} \int\limits_\gamma \frac{[\mathbf j(\mathbf r);\mathbf{r} - \mathbf{r}_0]}{|\mathbf r - \mathbf{r}_0 |^3} dV](http://upload.wikimedia.org/math/a/3/b/a3b2605327414de6ec95d7aafe3ac6ab.png)


