Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
Здесь
- ρ — плотность жидкости,
- v — скорость потока,
- h — высота, на которой находится рассматриваемый элемент жидкости,
- p — давление.
Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.
Это соотношение, выведенное Даниилом Бернулли в 1738 г., было названо в его честь уравнением Бернулли. (Не путать с дифференциальным уравнением Бернулли.)
Для горизонтальной трубы h = 0 и уравнение Бернулли принимает вид:  .
Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности ρ:  .
Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.
Полное давление состоит из весового (ρgh), статического (p) и динамического ( ) давлений.
Из закона Бернулли следует, что при уменьшении сечения потока, из-за
возрастания скорости, то есть динамического давления, статическое
давление падает. Это является основной причиной эффекта Магнуса.
Закон Бернулли справедлив и для ламинарных потоков газа. Явление
понижения давления при увеличении скорости потока лежит в основе работы
различного рода расходомеров, водо- и пароструйных насосов.
Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость
которых равна нулю, то есть таких жидкостей, которые не прилипают к
поверхности трубы. На самом деле экспериментально установлено, что
скорость жидкости на поверхности твердого тела всегда в точности равна
нулю.
Одно из применений
Закон Бернулли можно применить к истечению идеальной несжимаемой
жидкости через малое отверстие в боковой стенке или дне широкого сосуда.
Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:
 ,
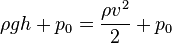где
- p0 — атмосферное давление,
- h — высота столба жидкости в сосуде,
- v — скорость истечения жидкости.
Отсюда: 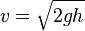 . Это — формула Торричелли.
Она показывает, что при истечении идеальной несжимаемой жидкости из
отверстия в широком сосуде жидкость приобретает скорость, какую
получило бы тело, свободно падающее с высоты h.
Для сжимаемого идеального газа
 [1] (постоянна вдоль линии тока или линии вихря)
где
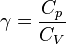 — Адиабатическая постоянная газа- p — давление газа в точке
- ρ — плотность газа в точке
- v — скорость течения газа
- g — ускорение свободного падения
- h — высота относительно начала координат
При движении в неоднородном поле gz заменяется на потенциал гравитационного поля.
| 
