Зако́н Архиме́да: на тело, погружённое[1] в жидкость (или газ, или плазму), действует выталкивающая сила (называемая силой Архимеда)
где ρ — плотность жидкости (газа),  — ускорение свободного падения, а V —
объём погружённого тела (или часть объёма тела, находящаяся ниже
поверхности). Выталкивающая сила (называемая также архимедовой силой)
равна по модулю (и противоположна по направлению) силе тяжести,
действовавшей на вытесненный телом объём жидкости (газа), и приложена к
центру тяжести этого объёма.
— ускорение свободного падения, а V —
объём погружённого тела (или часть объёма тела, находящаяся ниже
поверхности). Выталкивающая сила (называемая также архимедовой силой)
равна по модулю (и противоположна по направлению) силе тяжести,
действовавшей на вытесненный телом объём жидкости (газа), и приложена к
центру тяжести этого объёма.
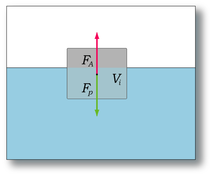
|Тело, помещённое в воду, | |плавает, если сила Архимеда| |уравновешивает вес тела. |
-------------------------------------
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что его плотность, плотность самого газа, меньше чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.
- PB − PA = ρgh
- FB − FA = ρghS = ρgV,
где PA, PB — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.
В теоретической физике также применяют закон Архимеда в интегральной форме:
 , где S — площадь поверхности, p — давление в произвольной точке, интегрирование производится по всей поверхности тела.
, где S — площадь поверхности, p — давление в произвольной точке, интегрирование производится по всей поверхности тела.
В отсутствии поля силы тяжести, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: проводящее тело вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление жидкости на глубине h есть p = ρgh. При этом считаем давление жидкости и напряжённость гравитационного поля постоянными величинами, а h — параметром. Возьмём тело произвольной формы, имеющее ненулевой объем. Введём правую ортонормированную систему координат Oxyz, причём выберем направление оси z совпадающим с направлением вектора 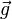 . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку dS. На неё будет действовать сила давления жидкости направленная внутрь тела,
. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку dS. На неё будет действовать сила давления жидкости направленная внутрь тела,  . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
Получаем, что модуль силы Архимеда равен ρgV, а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Примечания
- ↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, вблизи поверхности планеты).





