|
Зако́ны Ке́плера — семейство физических законов, открытых Иоганном Кеплером, описывающих движение планет вокруг Солнца. Первый закон Кеплера (Закон эллипсов)
Каждая планета Солнечной системы обращается по эллипсy, в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением 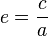 , где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.
Доказательство первого закона Кеплера Второй закон Кеплера (Закон площадей)
Каждая планета движется в плоскости, проходящей через центр
Солнца, причём за равные времена радиус-вектор, соединяющий Солнце и
планету, заметает сектора равной площади. Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий
— наиболее удалённая точка орбиты. Таким образом, из второго закона
Кепплера следует, что планета движется вокруг Солнца неравномерно, имея
в перигелии бо́льшую линейную скорость, чем в афелии. Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике
к востоку также происходит быстрее, чем в среднем за год. В начале июля
Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца
по эклиптике замедляется. Закон площадей указывает, что сила,
управляющая орбитальным движением планет, направлена к Солнцу.
Доказательство второго закона Кеплера Третий закон Кеплера (Гармонический закон) Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.  , где T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит. Ньютон установил, что гравитационное притяжение
планеты определенной массы зависит только от расстояния до неё, а не от
других свойств, таких, как состав или температура. Он показал также,
что третий закон Кеплера не совсем точен — в действительности в него
входит и масса планеты:  , где M – масса Солнца, а m1 и m2 – массы планет. Поскольку движение и масса оказались связаны, эту комбинацию
гармонического закона Кеплера и закона тяготения Ньютона используют для
определения массы планет и спутников, если известны их орбиты и
орбитальные периоды.
Доказательство третьего закона Кеплера
Второй закон Кеплера утверждает, что радиус-вектор обращающегося
тела заметает равные площади за равные промежутки времени. Если теперь
мы возьмём очень малые промежутки времени в момент, когда планета
находится в точках A и B (перигелий и афелий),
то мы сможем аппроксимировать площадь треугольниками с высотами,
равными расстоянию от планеты до Солнца, и основанием, равным
произведению скорости планеты на время.
Используя закон сохранения энергии для полной энергии планеты в точках A и B, запишем
Теперь, когда мы нашли VB, мы можем найти секториальную скорость. Так как она постоянна, то можем выбрать любую точку эллипса: например, для точки B получим
Однако полная площадь эллипса равна  (что равно πab, поскольку  ). Время полного оборота, таким образом, равно
Заметим, что если масса m не пренебрежимо мала по сравнению с M,
то планета будет обращаться вокруг Солнца с той же скоростью и по той
же орбите, что и материальная точка, обращающаяся вокруг массы M + m (см. приведённая масса). При этом массу M в последней формуле нужно заменить на M + m:
Современный уточненный третий закон Кеплера, учитывая
эксцентриситеты орбит, дает самую большую точность расчетов по небесной
механике и астрофизике: 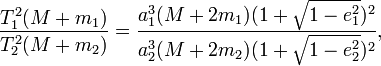 где e1,e2 - эксцентриситеты орбит. |
и 
во второе уравнение, получим 
, которая является удельным угловым моментом (
).Пусть 
становится равным 
![u = \frac{GM}{\ell^2} \left[ 1 + e\cos(\theta-\theta_0) \right] .](http://upload.wikimedia.org/math/e/1/d/e1de7bd8772f6b459768424ccab8e86c.png)
точечной частицы с массой 
записывается в виде: 
.
- радиус-вектор частицы а 
- импульс частицы. 
.
.
- константа. 
