Зако́н Ома — это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома. Суть закона проста: сила тока в проводнике прямо пропорциональна напряжению между концами проводника, если при прохождении тока свойства проводника не изменяются. Следует также иметь в виду, что закон Ома является фундаментальным и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков и т. д., также, как и Правила Кирхгофа, однако, такое приложение этого закона используется крайне редко в рамках узко специализированных расчётов.
| Ток, А| |
Напряжение, В| |
Сопротивление, Ом | | Мощность, Вт |
|---|---|---|---|
| I | U | R | P |
История закона Ома
Георг Ом, проводя эксперименты с проводником, установил, что сила тока I в проводнике пропорциональна напряжению U, приложенному к его концам:
 ,
,
или
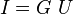 .
.
Коэффициент пропорциональности  назвали электропроводностью, а величину
назвали электропроводностью, а величину  принято именовать электрическим сопротивлением проводника.
принято именовать электрическим сопротивлением проводника.
Закон Ома был открыт в 1827 году.
Закон Ома в интегральной форме
 Схема, иллюстрирующая три составляющие закона Ома
Схема, иллюстрирующая три составляющие закона Ома
Закон Ома для участка электрической цепи имеет вид:
- U = RI
где:
- U — напряжение или разность потенциалов,
- I — сила тока,
- R — сопротивление.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
 ,
,
где:
 — ЭДС цепи,
— ЭДС цепи,- I — сила тока в цепи,
- R — сопротивление всех элементов цепи,
- r — внутреннее сопротивление источника питания.
Закон Ома в дифференциальной форме
Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
где:
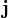 — вектор плотности тока,
— вектор плотности тока,- σ — удельная проводимость,
 — вектор напряжённости электрического поля.
— вектор напряжённости электрического поля.
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).
Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.
Закон Ома для переменного тока
Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:
где:
- U = U0eiωt — напряжение или разность потенциалов,
- I — сила тока,
- Z = Re—iδ — комплексное сопротивление (импеданс),
- R = (Ra2+Rr2)1/2 — полное сопротивление,
- Rr = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
- Rа — активное (омическое) сопротивление, не зависящее от частоты,
- δ = —arctg Rr/Ra — сдвиг фаз между напряжением и силой тока.
При этом переход от комплексных переменных в значениях тока и
напряжения к действительным (измеряемым) значениям может быть
произведен взятием действительной или мнимой части (но во всех
элементах цепи одной и той же!) комплексных значений этих величин.
Соответственно, обратный переход строится для, к примеру, U = U0sin(ωt + φ) подбором такой  , что
, что  . Тогда все значения токов и напряжений в схеме надо считать как
. Тогда все значения токов и напряжений в схеме надо считать как 
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.
Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
Объяснение закона Ома
Закон Ома можно просто объяснить при помощи теории Друде






