Физика. - Законы Ньютона

	Пятница, 26.04.2024, 07:42

	Главная Законы Ньютона Регистрация Вход

Приветствую Вас Гость | RSS

Меню сайта

	Главная страница Информация о сайте Каталог файлов Каталог статей Форум Фотоальбомы Обратная связь Что такое физика? Список физических законов Ключевые статьи по разделам физики Законы сохранения Закон сохранения момента импульса

Наш опрос

	Оцените мой сайт Отлично Хорошо Неплохо Плохо Ужасно Результаты \| Архив опросов Всего ответов: 1279

Законы Нью́тона — законы классической механики, позволяющие записать уравнения движения для любой механической системы.

Первый закон Ньютона

Инерциальной называется та система отсчёта, относительно которой любая, изолированная от внешних воздействий, материальная точка либо покоится, либо сохраняет состояние равномерного прямолинейного движения.
Первый закон Ньютона гласит:

Инерциальные системы отсчёта существуют.

По сути, этот закон постулирует инерцию тел, что сегодня кажется очевидным. Но это было далеко не так на заре исследования природы. Аристотель вот утверждал, что причиной всякого движения является сила, т. е. движения по инерции для него не существовало. ^{[источник?]}

Второй закон Ньютона

Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и её ускорением.

Второй закон Ньютона утверждает, что

в инерциальной системе отсчета (ИСО) ускорение, которое получает материальная точка, прямо пропорционально приложенной силе и обратно пропорционально массе.

При подходящем выборе единиц измерения этот закон можно записать в виде формулы:

$\vec a = \frac {\vec {F}} {m} ,$

где $\vec a$ — ускорение тела;

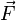$\vec {F}$ — сила, приложенная к телу;

$m$ — масса тела.

Или в более известном виде:

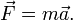
$\vec {F} = m \vec a .$

Если на тело действуют несколько сил, то второй закон Ньютона записывается:

$\sum_{i=1}^{n} {\vec{F_i}} = m \vec a$

или

$t \cdot \sum_{i=1}^{n} {\vec{F_i}} = \Delta\vec p,$

где $\vec p$ — импульс тела.

В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется в общем виде: скорость изменения импульса точки равна действующей на неё силе.

$\frac{d(m\vec v)}{dt} = \vec{F},$

где $m\vec v$ — импульс (количество движения) точки;

$t$ — время;

$\frac{d}{dt}$ — производная по времени.

Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.

Нельзя рассматривать частный случай (при $\vec {F} = 0$ ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Третий закон Ньютона

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой $\vec{F}_{1 \to 2}$ , а второе — на первое с силой $\vec{F}_{2 \to 1}$ . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

Сам закон:

Тела действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению:

$\vec{F}_{2 \to 1} = -\vec{F}_{1 \to 2}.$

Выводы

Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел $U ( | r 1 - r 2 | )$ . Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:

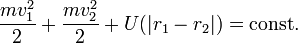
${m {v}_1^2 \over 2} + {m {v}_2^2 \over 2} + U(|{r}_1 - {r}_2|) = \operatorname{const}.$

Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.

Комментарии к законам Ньютона

Силы инерции

Законы Ньютона, строго говоря, справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона. Однако часто, для упрощения рассмотрения, вводят некую фиктивную «силу инерции», и тогда эти уравнения движения переписываются в виде, очень похожем на второй закон Ньютона. Математически здесь всё корректно (правильно), но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального взаимодействия. Ещё раз подчеркнём: «сила инерции» — это лишь удобная параметризация того, как отличаются законы движения в инерциальной и неинерциальной системах отсчета.

Законы Ньютона и Лагранжева механика

Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было минимальным), и из этого можно вывести все законы Ньютона. Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет

Решение уравнений движения

Уравнение $\vec {F} = m \vec a$ (то есть второй закон Ньютона) является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.

Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.

Форма входа

Календарь новостей

Поиск

Друзья сайта

Graffiti Decorations(R) Studio (TM) Site Promoter

Статистика

	Онлайн всего: 1 Гостей: 1 Пользователей: 0