Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности.
Для тонкого растяжимого стержня закон Гука имеет вид: 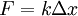 . Здесь  сила натяжения стержня,  — его удлинение, а  называется коэффициентом упругости (или жёсткостью).
Очевидно, что коэффициент упругости зависит как от свойств
материала, так и от размеров стержня. Полезно выделить зависимость от
размеров стержня (площади поперечного сечения 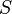 и длины  ) явно, записав коэффициент упругости как  . Величина  называется модулем Юнга и зависит только от свойств материала. Полезно теперь ввести относительное удлинение 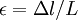 и нормальное напряжение в поперечном сечении  . В этих обозначениях закон Гука записывается как  . Величину, обратную жёсткости, называют гибкостью.
Обобщённый закон Гука
В общем случае напряжения и деформации являются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонентов). Связывающий их тензор упругих постоянных является тензором четвёртого ранга 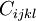 и содержит 81 коэффициент. Вследствие симметрии тензора 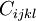, а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:
Для изотропного материала тензор 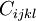содержит только два независимых коэффициента.
Следует иметь ввиду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности
связь между напряжениями и деформациями становится нелинейной. Для
многих сред закон Гука неприменим даже при малых деформациях.
| 
